상호배타적 집합(Disjoint Set)
오리엔테이션이나 수학 여행 등에서 서로 친해지기 위해서 하는 활동 중에 이런 활동들을 한번쯤 해보셨을 겁니다. 다들 서로 낯서고 모르는 상태이기 때문에 어색어색하죠. 이 순간은 서로가 각각 혼자서 있습니다. 그럴때 사회자가 혈액형이 같은 사람끼리 모이라고 했을때, A, B, AB, O 형으로 나뉘어진 각 사람들은 같은 혈액형을 찾으려고 시도하겠죠? 그래서 같으면 같은 조로 묶이게 됩니다.
이처럼 같은 특성끼리 서로 모이는 집합이 여러 집합이 있는데, 각 집합에서는 공통 원소가 존재하지 않는 그런 집합을 상호배타적 집합(Disjoint Set)이라고 합니다. 한 집합에서 다른 특성을 갖는 집합을 배제한다는 뜻입니다. 이때 쓰이는 자료구조가 유니온-파인드(Union-Find) 자료구조라고 합니다.
구현
상호배타적 집합을 구현하기 위해서는 트리의 자료구조를 사용합니다. 각 트리 노드들은 루트 노드를 가지고 있지요. 그래서 그 루트노드를 기준으로 같다면 같은 집합에 속해있는 것이고, 다르다면 다른 집합에 속해있다는 것을 알 수 있습니다.
1. 초기화
초기의 상태는 각 노드들이 자신이 루트가 됩니다. 아직 어떤 노드도 만난적이 없으니까 집합에서의 리더는 자기 자신일테니까요. 그러다가 같은 속성이 있다면 서로를 합치게 되는 것이죠. 아래의 코드가 초기화 코드를 나타냅니다. parent는 자신의 상위 트리 노드를 말하며 처음에는 자기 자신이 됩니다. 나머지 rank 변수는 이 후 설명하도록 하겠습니다.
struct DisjointSet {
vector<int> parent, rank;
DisjointSet(int n) :parent(n), rank(n, 1) {
for (int i = 0; i < n; i++)
parent[i] = i;
}
};
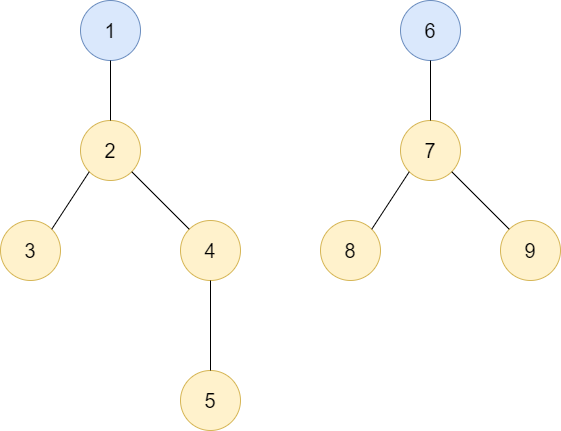
아래는 두 트리가 있음을 보여줍니다. 두 트리의 루트는 1과 6이라서 이 트리들은 서로 다른 집합을 나타내는 것이라고 할 수 있습니다.
2. 루트 찾기
여기서 각 루트를 찾는 코드는 아래와 같습니다.
int find(int node) {
if (node == parent[node]) return node;
return parent[node] = find(parent[node]);
}
find는 현재 노드가 속해있는 트리의 루트를 구하는 함수인데요. 여기서 재귀적으로 find를 호출해서 부모를 계속 찾다보면 나중에는 결국 부모가 자기 자신인 노드를 발견하게 됩니다. 왜냐면 루트의 부모는 없으며 루트는 위의 초기화에서 자기 자신이 부모 노드입니다. 그리고 반복적으로 find를 계속 호출하지 않기 위해서 parent[node] = find(parent[node]) 로 부모를 계산된 루트로 기록해둡니다. 그러면 나중에 루트를 찾을때 단번에 루트로 가서 반환되게 때문에 최적화를 할 수 있습니다.
3. 트리 합치기
루트가 다른 이 트리, 알보고니 공통 속성이 있어서 합쳐야될 것 같습니다. 합쳐보긴할텐데 어느쪽으로 합쳐야될까요? 우리는 루트가 1인 트리를 루트가 6인 트리에 합쳐야할까요? 아니면 6인 트리를 1인 트리 밑으로 가게 만들까요? 우리가 find를 구현했을때 루트를 찾이 위해서 계속 재귀적으로 부모를 호출해가면서 확인해보았습니다.
그렇다면 루트를 빨리 찾기 위해서는 노드의 부모수가 적으면 속도가 빨라지겠죠. 그런 원리로 최적화하면 됩니다. 즉, 트리의 높이를 작게 만들수록 유리합니다.

1이 루트인 트리에 6이 루트인 트리를 밑에 합쳐놓은 상황입니다. 트리의 높이가 증가했음을 알 수 있죠? 그렇다면 반대로 합쳐놓는다면, 즉 6이 루트인 트리에 1이 루트인 트리를 보면 어떨까요?
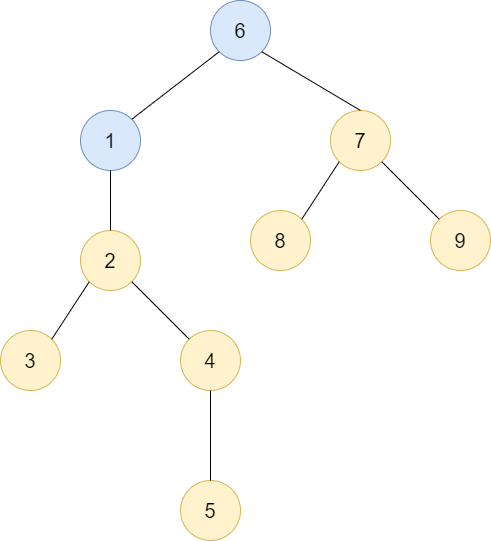
아래의 그림이 그 상황을 보여줍니다. 트리의 높이가 증가하지 않았음을 볼 수 있습니다. 그렇다면 결국에는 트리의 높이가 큰 트리 밑에 작은 트리를 합쳐 놓는게 높이를 증가시키지 않는 방법이네요. 이제 구현해봅시다.
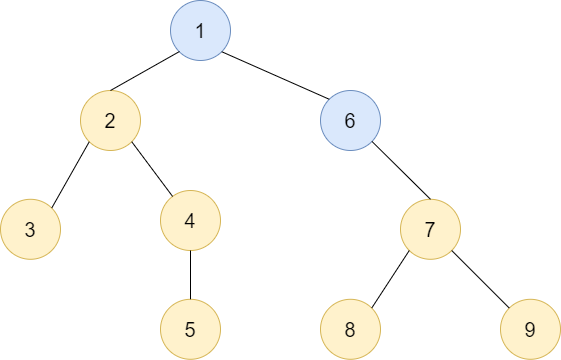
아래의 구현이 병합하는 코드를 구현한 것입니다.
void merge(int left, int right) {
left = find(left), right = find(right);
if (left == right) return;
if (rank[left] > rank[right]) swap(left, right);
parent[left] = right;
if (rank[left] == rank[right]) ++rank[right];
}
왼쪽 트리가 항상 오른쪽 트리의 자식이 될 수 있도록 구현한 코드인데요. 왼쪽 트리의 루트를 구하고, 오른쪽 트리의 루트를 구해서 같으면 이미 같은 트리에 속해있는 것으로 종료합니다.
그 후 rank라는 배열을 통해서 트리의 높이를 얻어옵니다. 항상 왼쪽에 작아서 오른쪽으로 합칠 구현을 해야하니까 값이 왼쪽이 크다면 교환해줍니다. 그래서 결국 왼쪽 부모는 오른쪽의 부모와 같게 만들죠.
트리의 높이가 증가하는 경우는 왼쪽, 오른쪽 트리의 rank값이 같을때만 존재합니다.
전체 소스코드는 아래와 같게됩니다. 아래의 코드는 알고리즘 문제해결 전략, 구종만 님의 코드를 참고했습니다.
struct DisjointSet {
vector<int> parent, rank;
DisjointSet(int n) :parent(n), rank(n, 1) {
for (int i = 0; i < n; i++)
parent[i] = i;
}
int find(int node) {
if (node == parent[node]) return node;
return parent[node] = find(parent[node]);
}
void merge(int left, int right) {
left = find(left), right = find(right);
if (left == right) return;
if (rank[left] > rank[right]) swap(left, right);
parent[left] = right;
if (rank[left] == rank[right]) ++rank[right];
}
};
예제 : BOJ 1717번, 집합의 표현
정확한 이해를 돕기 위해서 아래의 문제를 풀어봅시다. DisjointSet을 이용해서 풀 수 있는 문제로 위의 동작을 이해할 수 있으면 거뜬하게 풀 수 있는 문제입니다.
1717번: 집합의 표현
첫째 줄에 n(1 ≤ n ≤ 1,000,000), m(1 ≤ m ≤ 100,000)이 주어진다. m은 입력으로 주어지는 연산의 개수이다. 다음 m개의 줄에는 각각의 연산이 주어진다. 합집합은 0 a b의 형태로 입력이 주어진다. 이는
www.acmicpc.net
문제의 입력은 아래와 같습니다.
7 8
0 1 3
1 1 7
0 7 6
1 7 1
0 3 7
0 4 2
0 1 1
1 1 1
처음 N과 M이 주어지며 N은 집합의 원소 중 가장 마지막 원소, M은 질의를 나타냅니다.
다음은 질의가 M가 나오는데 질의의 유형은 0 a b, 1 a b가 있습니다. 0 a b는 a가 포함된 집합, b가 포함된 집합을 합치는 연산이며 1 a b는 a와 b가 같은 집합에 속해있는지 확인하는 연산입니다. 이때 1 a b의 질의에서 같은 집합에 속한다면 YES를 출력, 아니면 NO를 출력하면 됩니다.
위의 입력에 대한 출력은 아래와 같습니다.
NO
NO
YES
풀이
맨 처음에는 각각의 수들은 다른 집합에 속해있다가 연산 0이 나오면 합치면 됩니다. 이 역할이 DisjointSet의 merge가 되겠군요. 그리고 연산 1이면 a와 b가 같은 집합에 속해있는지 확인하는 연산이므로 find(a), find(b)를 통해 두 집합의 root를 구한후 같은지 다른지 확인하면 되는 간단한 문제입니다.
문제의 정답 코드는 이렇습니다.
#include <cstdio>
#include <vector>
using namespace std;
#define MERGE 0
#define SAME_GROUP 1
struct DisjointSet {
vector<int> parent, rank;
DisjointSet(int n) :parent(n), rank(n, 1) {
for (int i = 0; i < n; i++)
parent[i] = i;
}
int find(int node) {
if (node == parent[node]) return node;
return parent[node] = find(parent[node]);
}
void merge(int left, int right) {
left = find(left), right = find(right);
if (left == right) return;
if (rank[left] > rank[right]) swap(left, right);
parent[left] = right;
if (rank[left] == rank[right]) ++rank[right];
}
};
int main() {
int N, M;
scanf("%d %d", &N, &M);
DisjointSet djs(N+1);
for (int i = 0; i < M; i++) {
int query, a, b;
scanf("%d %d %d", &query, &a, &b);
if (query == MERGE) djs.merge(a, b);
if (query == SAME_GROUP)
printf("%s\n", djs.find(a) == djs.find(b) ? "YES" : "NO");
}
}
이상으로 상호배타적 집합에 대한 개념과 코드 구현, DisjointSet을 이용해서 문제를 풀어보았습니다. DisjointSet 알고 있으면 도움이 될 것 같나요?
'자료구조' 카테고리의 다른 글
| [스택] BOJ17298 오큰수 문제 풀이 및 전체 코드(C++) (3) | 2022.01.26 |
|---|---|
| [스택] BOJ 2504 괄호의 값 - 그림으로 보는 풀이 및 코드 (0) | 2021.04.21 |
| [자료구조] 해시 개념과 정적 해시 설명 및 오버플로 핸들링(overflow handling)) (1) | 2021.02.27 |
| [자료구조] 스택 응용 전위표기(prefix), 후위표기(postfix), 중위표기(infix) (1) | 2019.01.23 |
| [자료구조] 구간트리 (Segment Tree) 개념과 구현 (0) | 2018.12.09 |



