구간트리(Segment Tree)
구간트리는 특정 구간에서 특정한 값을 뽑아올때 유용하게 사용됩니다. 세그먼트트리라고도 하지요. 한 가지 예를 들어보도록 할게요. 어떤 배열이 아래와 같이 있다고 치구요.
int arr[] = {7, 4, 5, 1, 9, 5, 2, 11, 10};
0번 요소부터 5번째 요소까지의 가장 작은 값은 얼마인가요? 1이네요. 그쵸?
그렇다면 2번 요소부터 7번째 요소까지 가장 큰 값은 얼마일까요? 11이 됩니다.
어떻게 찾을 수 있죠? 구간트리를 배우지 않았다면 for루프를 통해서 가장 작은 값이나 가장 큰 값을 구할겁니다.
for (i = from; i <= to; i++) {
minVal = min(arr[i], minVal);
}
이렇게 말이죠. 아주 쉽네요!! 시간 복잡도는 O(n)입니다.
하지만 구간에서 가장 작은 값을 계속해서 뽑아내야하는 상황이라면 구간트리를 사용해야합니다. 구간트리를 사용한다면 최소, 최대값을 찾는데 O(log n)이면 충분합니다.
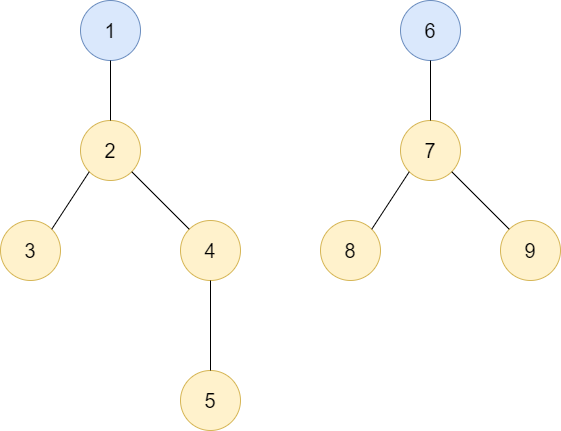
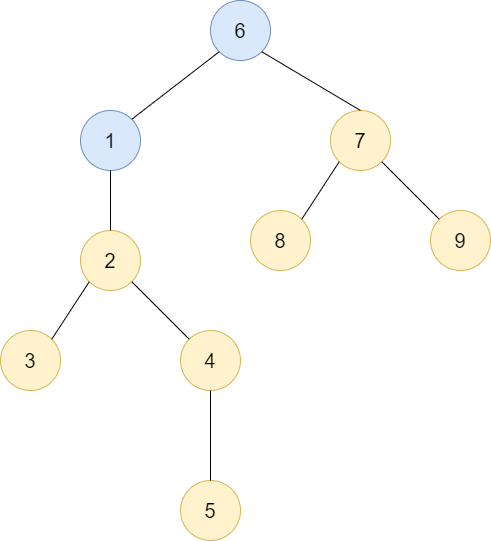
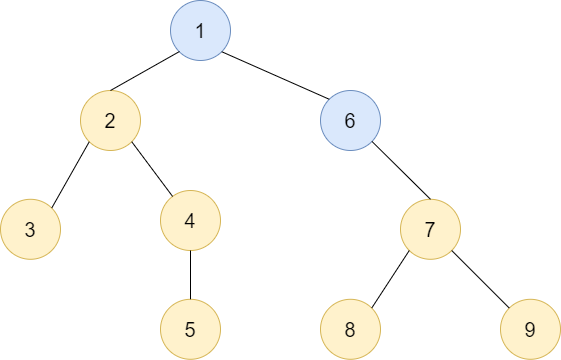
구간트리의 노드는 특정 구간에서 가장 작은 값을 가지고 있습니다. 아래 트리가 구간 트리를 보여줍니다. 위의 배열을 구간트리로 표현한 모습이죠.

파란색 원 안의 숫자는 노드의 번호, 사각형 안의 숫자는 배열의 범위를 나타냅니다. 우리는 트리를 배열로 표현하기 위해서 가장 첫번째(root)는 1번 인덱스를 갖습니다. 자식 노드의 번호는 2와 3이 됩니다.
그렇다면 어떤 노드 i의 왼쪽 자식은 i*2, 오른쪽 자식은 i*2+1이 되는 것이죠.
우리가 3번 요소부터 7번 요소까지 가장 작은 값을 갖는 값을 뽑아오려면 5번, 6번, 14번 노드를 통해서 구할 수 있습니다.
이제 본격적으로 구현해보도록 합시다.
구현(C++)
구간 트리에서 특정 구간에서 최소값을 찾는 것을 구간 최소 트리(Range Minimum Query, RMQ) 라고 합니다. 그래서 이 구조체를 만드는 것에서부터 시작합니다.
struct RMQ {
int size;
vector<int> minValues;
RMQ(int *arr,int arrSize) {
size = arrSize;
minValues.resize(size * 4);
init(arr, 0, size - 1,1);
}
}
size는 배열의 size를 의미합니다. minValues는 해당 노드에서 가장 작은 값을 저장하는 벡터입니다.
왜 minValues의 사이즈를 배열의 사이즈 * 4를 할까요? 위의 트리를 다시 보게 되면 배열의 크기보다 많은 노드를 볼 수 있습니다. 완전 이진 트리를 아신다면 마지막 leaf의 개수 * 2가 트리의 노드수를 의미한다는 것을 알겁니다.
하지만 귀찮으니 4를 곱하면 된다고 하네요.
이제 이 구조체를 초기화하는 함수 init을 불러서 구간트리의 모양을 잡아보도록 합시다.
init
잘 생각해보면 간단합니다. 왼쪽 자식, 오른쪽 자식의 값을 비교해서 가장 작은 값이 지금 이 노드의 값이 됩니다.
만약 leaf노드까지 도달했다면 그 값만을 반환해주면 되죠.
그리고 구간트리의 인덱스 node라는 값도 함께 넘겨주어 현재 노드에 가장 작은 값을 저장할 수 있게끔 하면 됩니다.
int init(int *arr, int left, int right,int node) {
if (left == right) return minValues[node] = arr[left];
int mid = (left + right) / 2;
int leftMinValue = init(arr, left, mid, node * 2);
int rightMinValue = init(arr, mid + 1, right, node * 2 + 1);
return minValues[node] = min(leftMinValue, rightMinValue);
}
query
이 함수는 질의, 즉 물어보는 함수입니다. 특정 구간에 가장 작은 값을 반환하여라! 라고 질문을 던져 답을 받습니다. 이 함수도 역시 잘 생각해보면 별 어려움은 없습니다.
질의하는 범위가 노드가 커버할 수 있는 범위를 완전히 포함한다면 그 값을 내주면 됩니다.
그것이 아니라면 아주 큰 값을 리턴하면 되지요.
만약 위의 배열에서 3-7 구간에 대해 질의를 한다면 5번, 6번, 14번 노드가 3-7구간에 완전히 포함되므로 그 세개의 노드만이 자신의 값을 반환합니다. 그 후 가장 작은 값이 답이 되겠죠?
헷갈릴 수 있습니다. 노드가 커버하는 범위가 질의하는 범위에 완전히! 속해있어야합니다.
int query(int left, int right, int node, int nodeLeft, int nodeRight) {
if (right < nodeLeft || nodeRight < left) return INF;
if (left <= nodeLeft&&nodeRight <= right)
return minValues[node];
int mid = (nodeLeft + nodeRight) / 2;
int leftMinValue = query(left, right, node * 2, nodeLeft, mid);
int rightMinValue = query(left, right, node * 2 + 1, mid + 1, nodeRight);
return min(leftMinValue, rightMinValue);
}
너무 함수가 섹시하지가 않군요. 인자가 너무 많습니다. C++에 지원되는 오버로딩을 사용하여 좀 더 간편하게 부를 수 있도록 하죠.
int query(int left, int right) {
return query(left, right, 1, 0, size - 1);
}
update
구간 트리에서 값이 바뀌면 구간의 최소값도 바뀌어여합니다. 특정 index와 새로운 value를 받게되면 구간트리의 해당 노드의 값을 바꾸고 차례대로 값을 갱신해주어야합니다. 여기서 노드의 값이 바뀌는 순서는 해당 leaf노드부터 루트까지 올라오게 됩니다.
만약 5번 인덱스가 새로운 값으로 바뀌게 되었다면 해당하는 노드의 번호 12번노드부터 6번 노드, 3번 노드, 1번 노드가 갱신되어야 하죠.
int update(int index, int value, int node, int nodeLeft, int nodeRight) {
if (index < nodeLeft || nodeRight < index) return minValues[node];
if (nodeLeft == nodeRight) return minValues[node] = value;
int mid = (nodeLeft + nodeRight) / 2;
int leftMinValue = update(index, value, node * 2, nodeLeft, mid);
int rightMinValue = update(index, value, node * 2 + 1, mid + 1, nodeRight);
return minValues[node]=min(leftMinValue, rightMinValue);
}
그러니까 nodeLeft==nodeRight가 같은 경우, 즉 해당하는 leaf인 경우 그 노드의 값을 갱신합니다.index의 범위 밖이면 그냥 가지고 있는 값을 반환해주면 되고, index가 포함되어 있는 경우라면 왼쪽 자식 값, 오른쪽 자식 값을 비교해서 가장 작은 값을 갖게 해주면 됩니다.
int update(int index, int value) {
return update(index, value, 1, 0, size - 1);
}
깔끔하게 함수를 호출할 수 있도록 오버로딩했구요.
전체코드
#include <iostream>
#include <vector>
#include <algorithm>
#define INF 99999999
using namespace std;
struct RMQ {
int size;
vector<int> minValues;
RMQ(int *arr,int arrSize) {
size = arrSize;
minValues.resize(size * 4);
init(arr, 0, size - 1,1);
}
int init(int *arr, int left, int right,int node) {
if (left == right) return minValues[node] = arr[left];
int mid = (left + right) / 2;
int leftMinValue = init(arr, left, mid, node * 2);
int rightMinValue = init(arr, mid + 1, right, node * 2 + 1);
return minValues[node] = min(leftMinValue, rightMinValue);
}
int query(int left, int right, int node, int nodeLeft, int nodeRight) {
if (right < nodeLeft || nodeRight < left) return INF;
if (left <= nodeLeft&&nodeRight <= right)
return minValues[node];
int mid = (nodeLeft + nodeRight) / 2;
int leftMinValue = query(left, right, node * 2, nodeLeft, mid);
int rightMinValue = query(left, right, node * 2 + 1, mid + 1, nodeRight);
return min(leftMinValue, rightMinValue);
}
int query(int left, int right) {
return query(left, right, 1, 0, size - 1);
}
int update(int index, int value, int node, int nodeLeft, int nodeRight) {
if (index < nodeLeft || nodeRight < index) return minValues[node];
if (nodeLeft == nodeRight) return minValues[node] = value;
int mid = (nodeLeft + nodeRight) / 2;
int leftMinValue = update(index, value, node * 2, nodeLeft, mid);
int rightMinValue = update(index, value, node * 2 + 1, mid + 1, nodeRight);
return minValues[node]=min(leftMinValue, rightMinValue);
}
int update(int index, int value) {
return update(index, value, 1, 0, size - 1);
}
};
int main() {
int arr[] = { 7, 4, 5, 1, 9, 5, 2, 11, 10 };
RMQ rmq(arr, sizeof(arr) / sizeof(int));
printf("query(0-8) : %d\n", rmq.query(0, 8));
printf("query(1-6) : %d\n", rmq.query(1, 6));
printf("query(7-8) : %d\n", rmq.query(7, 8));
printf("query(3-7) : %d\n", rmq.query(3, 7));
printf("query(0-2) : %d\n", rmq.query(0, 2));
printf("query(0-2) : %d\n", rmq.query(4, 8));
printf("update(index 4, value 0)) : %d\n", rmq.update(4,0));
}
-- 내용과 코드는 구종만의 알고리즘 문제해결 전략을 참고했습니다