해싱(Hashing)
해싱(Hashing)은 데이터를 관리하는 고급 기법으로 검색(search), 삽입(insert), 삭제(delete)를 단시간(O(1))에 할 수 있게 만들어주는 기법입니다.
예를 들면, 리스트에서 단어를 찾는 시간이 O(n)시간이 걸리고, 이진 트리의 경우 O(nlogn)이 걸리죠. 그런데 우리는 이것을 해싱이란 기법을 사용하여 O(1)만에 해결할 수 있습니다. 진짜 죠낸 빠르네요.
해싱은 산술적 연산을 이용해서 구현해야합니다. 이런 해싱은 크게 두 가지 종류가 있는데요. 하나는 정적 해싱(static hasing)이고 다른 하나는 동적 해싱(dynamic hasing)입니다. 이번 포스팅은 정적 해싱에 대한 이야기를 합니다.
정적 해싱(Static Hashing)
정적 해싱이라는 기법은 고정 크기의 버킷을 갖는 해시 테이블(담을 그릇)에 데이터를 담는 것을 말합니다.
해시 테이블(Hash Table)
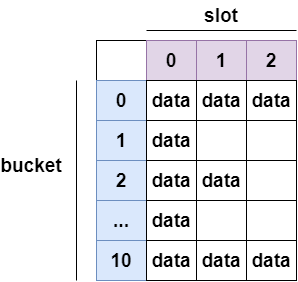
설명 전에 해시 테이블(Hash Table)에 관해서 알고 가야합니다. 해시 테이블은 키(Key)와 값(Value)으로 구성되어 있는 데이터가 저장된 테이블이라고 보시면 됩니다. 해시 테이블은 행과 열로 구성되어 있다고 생각하세요. 여기서 두 가지 용어가 있는데 버킷(bucket)과 슬롯(slot)입니다.
버킷(bucket) : 버킷은 해시 테이블의 행 인덱스(주소)라고 입니다.
슬롯(slot) : 슬롯은 그 행을 열의 인덱스(주소)라고 생각하시면 됩니다.
아래의 그림은 버킷이 11, 슬롯이 3인 해시 테이블입니다. 여기서 data가 전부 차있는 버킷도 존재하고 그렇지 않은 곳도 존재합니다. bucket[0]을 보시면 이미 데이터가 가득차있네요. 다음 들어올 데이터가 bucket[0]에 들어갈 데이터라면 어떻게 될까요? 넣을 수 없는 상황이 되겠죠?
그것을 우리는 오버플로(Overflow)라고 하며 이 문제를 해결해야합니다. 잠시후 설명하도록 하겠습니다.
쳐넣는거는 알겠는데 어떻게 넣냐구요? 해시 함수를 이용해서 넣을 수 있습니다.
해시 함수(Hash Function)
해시 함수는 h()라 하고 찾을 키를 k라고 한다면 해시 함수는 h(k)라 표현합니다. 해시 함수는 k를 이용해서 해시 테이블에 매핑(mapping)하는 역할을 하게 됩니다. 즉, 데이터를 집어넣을 장소(주소)를 정합니다. 좋은 해시 함수는 계산이 쉬워야하고, 출돌을 최소화 시켜야합니다. 그리고 모든 버킷에 데이터가 고르게 분포되어야합니다. 앞서말한 오버플로를 최소화하기 위함이죠. 해시 함수에는 어떤 것들이 있을까요?
참고로 아래의 해시함수들은 모두 키가 양의 정수를 갖는데, 만약 키를 문자나 문자열로 쓰고 싶다면 문자(열)을 정수로 변환시키는 작업이 필요합니다.
1) Division
나눗셈을 이용하는 해시 함수입니다. 모듈러 연산(나머지를 구하는 연산으로 % 아시죠?)을 이용하여 집어 넣을 곳을 정합니다. 키들은 음수이면 안된다는 가정이 있습니다.
h(k) = k % D
해시 테이블은 적어도 D개의 버킷을 가지고 있어야합니다. k가 15이고 D가 7이라면 h(15) = 15 % 7 = 1 이 됩니다.
2) Mid-Square
키를 제곱하여 버킷을 정하는 건데요. 키를 제곱한 후 중간에 몇 비트를 선택하여 버킷의 주소를 구합니다. r비트를 선택하면 해시 함수 결과로 나올 수 있는 값의 범위는 0 ~ (2^r) -1이 되겠죠?
r을 3로 정해보고, key값을 121으로 정해서 계산해보면 121^2 = 14,641인데 이것의 가운데 3개를 가져오면 h(121) = 464가 됩니다.
3) Folding
폴딩은 키를 몇몇 부분(Part)로 나눈후 그 값을 더하여 해시 함수의 결과를 도출합니다. 방식에 따라 두가지가 있는데요. 그냥 부분을 일정하게 나눈 후 더하는 방식인 시프트 폴딩(Shift Folding)과 부분의 경계를 뒤집어서 계산하는 경계폴딩(Boundary Folding)이 있습니다.
1. 시프트 폴딩(Shift Folding)
k가 12345678910일때 3개의 10진수로 나눈다면 h(12345678910) = 123 + 456 + 789 + 10이 되고 더하게 되면 1378이 되므로 h(12345678910) = 1,378 입니다.
2. 경계 폴딩(Boundary Folding)
k가 아까와 같이 12345678910이고 3개의 10진수로 나눈다면 h(12345678910) = 123 + 654 + 789 + 01이며 결과는 1,567입니다. 456과 10이 뒤집혀진 것을 알 수 있네요.
4) Digit Analysis
이 방식은 이미 모든 키들을 알고 있는 정적 파일에 유용한 방법으로 각 키의 주소를 결정할 때 많이 나오는 수는 제외하고 적게 나오는 키의 수만 선택됩니다.
예를 하나 들어보겠습니다. 키가 5개가 미리 정해져있다고 칩시다. 각 키는 0112311, 0234522, 0167811, 0291022, 0111222 에서 숫자 3개를 선택해서 해시 함수의 결과를 꺼내면 hash(0112311) = 123, hash(0234522) = 345, hash(0167811) = 678, hash(0291022)= 910, hash(0111222) = 112 가 됩니다. 01 11 02 22는 많이 겹치는 수이기 때문에 고르지 않습니다.
이름에서 알 수 있듯이 키의 숫자들을 분석을 해야하는데요. 분석하려면 미리 결정된 데이터들이 있어야합니다. 즉, 키가 미리 결정되어져 있어야한다는 의미입니다. 그러니까 왜 정적 파일에 유용한지 이해가 가시죠?
오버플로 핸들링(Overflow Handling)
앞서 오버플로에 대해서 이야기했었죠? 오버플로를 해결하기 위해서는 두 가지 핸들링 기법이 있는데, 개방 주소법(Open Address)과 체이닝(Chaining) 방식이 있습니다.
1) 개방 주소(Open Address)
오버플로가 발생했을때 공간이 남는 버킷에 집어 넣는 것으로 공간이 남는 버킷 어느 곳이나 있으면 넣는 다고 하여 개방 주소라고 합니다. 남는 곳을 어떻게 구햐냐에 따라 4 가지 방식이 존재합니다.
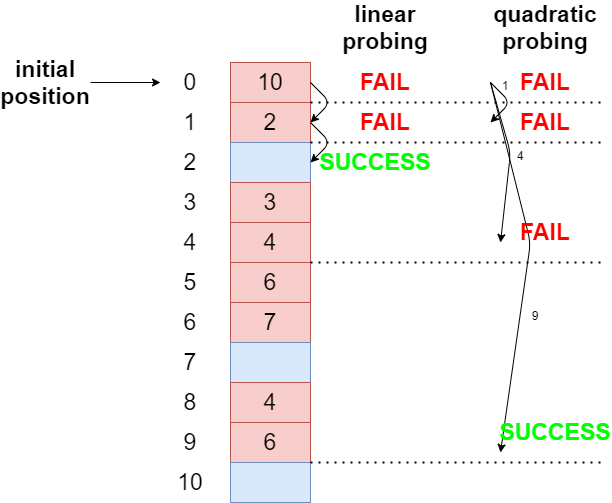
1. 선형 탐사(Linear Probing)
선형 탐사만 알아도 나머지 probing방식은 이해할 수 있습니다. 고정된 폭을 정해서 그 폭만큼 버킷의 주소를 이동해서 남는 공간이 있는지 확인 후에 있으면 집어넣는 방식입니다. 그래도 남는 공간이 없다면 다시 그 폭만큼 버킷의 주소를 이동하죠. 만약 해시 테이블의 공간이 모자란다면 해시 테이블의 크기를 증가시키는데, 전부 찰때 증가시키는 것이 아니고 75% 정도 채워지면 해시 테이블의 크기를 증가시킵니다.
만약 폭을 i라고 하고 버킷의 크기를 b라고 한다면 해시 테이블은 (h(k) + i ) % b 의 식으로 계산됩니다.
2. 제곱 탐사(Quadratic Probing)
감 오시죠? 폭을 제곱하여 오버플로를 핸들링합니다. (h(k) + (i^2)) %b 로 계산됩니다. 만약 오버플로가 발생하면 i=1로 한칸 이동하여 찾고 그래도 실패하면 그 다음은 i=2가 되어 4칸을 이동하고, 그 다음은 i=3이 되어 9칸을 이동하여 검사하는 방식입니다.
아래 그림은 선형 탐사와 제곱 탐사를 비교한 그림입니다.
3. 무작위 탐사(Qandom Probing)
감 오시죠? 랜덤한 값을 폭으로 두고 계산합니다.
4. 이중 해시(Double Hashing)
해싱한 값을 한 번 더 해싱하는 방식입니다. 다른 방식보다 연산하는 시간이 걸립니다. 해시 연산을 한 번 더 하기 때문이죠.
2) 체이닝(Chaining)
체이닝은 이름과 같이 체인같이 연결하여 오버플로를 막는 방법인데요. 연결 리스트(Linked List) 배우셨죠? 각 버킷이 연결 리스트가 되고 원소가 계속 추가 될 수 있습니다.
아래는 체이닝 기법을 적용한 버킷이 6개있는 해시 테이블입니다.
이때 삽입할때 연결리스트의 앞에 삽입합니다. 이유는 매번 끝에 원소를 삽입하면 연결리스트에 끝까지 도달해야되기 때문에 삽입 시간이 오래 걸리기 때문입니다.

개방주소법이나 체이닝 방식이나 최악의 경우(Worst Case) 성공할때까지 검색하는 시간은 O(n)의 시간이 걸릴 수 있습니다. 하지만 균형잡힌 검색 트리(Balanced Search Tree)를 이용하면 이 시간은 O(logn)까지 줄일 수 있습니다.
다음 포스팅은 동적 해싱에 대한 이야기를 하도록 하겠습니다.
'자료구조' 카테고리의 다른 글
| [스택] BOJ 2504 괄호의 값 - 그림으로 보는 풀이 및 코드 (0) | 2021.04.21 |
|---|---|
| [자료구조] 상호 배타적 집합(Disjoint Set)과 유니온-파인드(Union-Find) 자료구조의 개념과 구현, 예제 (0) | 2021.03.22 |
| [자료구조] 스택 응용 전위표기(prefix), 후위표기(postfix), 중위표기(infix) (1) | 2019.01.23 |
| [자료구조] 구간트리 (Segment Tree) 개념과 구현 (0) | 2018.12.09 |
| [자료구조] 그림으로 쉽게 보는 힙(Heap) 개념과 코드 (3) | 2018.12.01 |



