https://www.acmicpc.net/problem/17299
17299번: 오등큰수
첫째 줄에 수열 A의 크기 N (1 ≤ N ≤ 1,000,000)이 주어진다. 둘째에 수열 A의 원소 A1, A2, ..., AN (1 ≤ Ai ≤ 1,000,000)이 주어진다.
www.acmicpc.net
설명
문제에서 말하는 오등큰수는 이 수가 나타난 수보다 더 많이 나타난 수 중 가장 가까운 오른쪽 수를 의미합니다. 특정 수의 오등큰수가 없을 수가 있습니다. 이런 경우 그 수의 오등큰수는 -1로 정해줍니다. 문제의 예제는 이렇습니다.
A = [1, 1, 2, 3, 4, 2, 1]
우선 F(Ai)는 빈도수라고 하여 차례대로 빈도수를 구하면 이렇게 되겠네요.
F(1) = 3, F(2) = 2, F(3) = 1, F(4) = 1
이렇게 빈도수가 구해지면 NGF라는 오등큰수를 구할 수 있습니다. NGF(1)을 구하는데, 1보다 빈도수가 큰 수는 없으므로 NGF(1) = -1이 됩니다. NGF(2) = 1이됩니다. 왜냐면 2보다 빈번하게 나타난 수는 1이고 이 수가 가장 가까운 오른쪽에 있는 수가 되기 때문이죠. 예제의 답은 그래서 아래와 같습니다.
-1 -1 1 2 2 1 -1
풀이
이 문제는 스택으로 풀 수 있습니다. 우선 F(Ai)를 구해야하는데요. 이건 간단합니다. 비어있는 배열 F에 입력받은 수를 index삼아서 하나씩 증가시키면 되기 때문입니다. 이제 F를 구했으면 스택을 이용해서 본격적으로 문제를 풀어봅시다.
아래의 블록은 F를 나타냅니다. 높을 수록 F가 높다는뜻입니다.
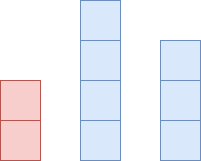
왼쪽의 빨간 블록의 오등큰수를 구하려면 오른쪽에서 찾아야합니다. 그런데 자신보다 큰 오등큰수가 두개가 있습니다. 4와 3이 있네요. 이때 빨간색의 오등큰수는 4가 됩니다. 이때 3은 이 다음 왼쪽 수의 오등큰수가 될 수 있을까요? 이미 4한테 막혀있고 4가 더 큰값이기 때문에 가능성이 없습니다. 그래서 3은 지워버립니다. 대신 4가 왼쪽의 오등큰수가 될 수 있는것을 알 수 있네요.
따라서 현재 자신보다 큰 값의 오등큰수가 존재하면 스택에 저장하고 작거나 같으면 스택에서 지워버리는 식으로 문제를 풀 수 있습니다.
코드
문제 해답에 대한 전체코드는 아래와 같습니다.
#include <cstdio>
#include <stack>
using namespace std;
int n;
int F[1000001], ans[1000001], nums[1000001];
stack<int> st;
int main() {
scanf("%d", &n);
for (int i = 0; i < n; i++) {
scanf("%d", &nums[i]);
F[nums[i]]++;
}
for (int i = n - 1; i >= 0; i--) {
int number = nums[i];
int height = F[number];
while (!st.empty()) {
int topNum = nums[st.top()];
int topHeight = F[topNum];
if (height >= topHeight) st.pop();
else break;
}
ans[i] = -1;
if (!st.empty()) ans[i] = nums[st.top()];
st.push(i);
}
for (int i = 0; i < n; i++)
printf("%d ", ans[i]);
printf("\n");
}
'알고리즘' 카테고리의 다른 글
| [알고리즘] 백준 BOJ 3986 좋은단어 풀이 및 코드 (0) | 2022.03.01 |
|---|---|
| [알고리즘] 최단거리 플로이드(Floyd) 알고리즘 (1) | 2019.01.06 |



