'BOJ1967'에 해당되는 글 1건

BOJ 1968 트리의 지름

https://www.acmicpc.net/problem/1967

이 문제는 가중치가 주어진 트리에서 leaf과 leaf 사이, 혹은 루트와 leaf 사이의 모든 가중치의 합 중 가장 큰 값을 구하는 문제입니다. 

예제에서 주어진 그래프에서는 45의 값으로 답이 됩니다. 빨간색 선을 따라가면 9 - 5 - 3 - 6 - 12의 노드를 지나게 되고 가중치 합은 45라는 것을 알 수 있습니다. 이 값보다 큰 값은 존재하지 않습니다.

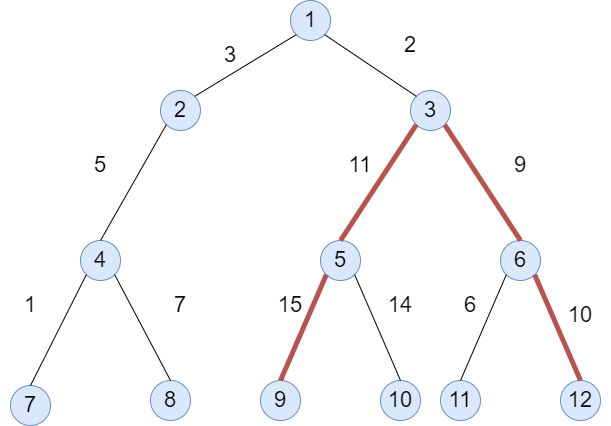
이 문제는 트리를 사용하여 풀 수 있습니다. 트리의 잎부터 시작해 올라오면서 서브트리의 양쪽 잎까지의 가중치 합과 서브트리의 루트와 잎까지 합 중 가장 큰 값으로 계속 업데이트를 하면 됩니다.

설명 및 전체 코드

입력받은 값으로 트리를 구성해야하는데, 이때 Node라는 구조체로 노드를 만들겠습니다. 이 Node 구조체는 자식 Node들을 가지고 있고, 부모로 향하는 weight값을 가지고 있는 구조체로 정의되어 있습니다. 노드의 자식은 여러개일 수 있으므로 vector를 사용했습니다.

typedef struct Node {
	vector<Node*> children = vector<Node*>();
	int weight;
};

기저사례로는 자식이 없을 경우 바로 부모로 향하는 weight를 return해줍니다. 더 이상 진행할 필요가 없으니까요. 그리고 자식이 한개일 경우에는 weight와 그 밑으로 향하는 큰 값중 하나를 더해서 반환해주면 됩니다.

if (root->children.size() == 0) return root->weight;

if (root->children.size() == 1) 
	return root->weight + traverse(root->children[0]);

그 외에는 자식이 둘 이상이겠죠. 양쪽으로 분기되는 값 중 가장 큰 값 두개를 선택해서 더해준 값을 현재까지 업데이트된 값하고 비교하여 둘 중 가장 큰 값으로 업데이트해줍니다. 현재까지 업데이트된 값을 value라고 임시로 정해줍시다.

이 과정을 루트로 올라올때까지 진행해주면 답을 구할 수 있습니다. 아래는 정답 코드입니다.

#include <cstdio>
#include <vector>
#include <algorithm>

using namespace std;

int n;
typedef struct Node {
	vector<Node*> children = vector<Node*>();
	int weight;
};

Node nodes[10001];
int value = 0;
int traverse(Node *root) {
	//자식이 없는 경우 부모쪽으로 가는 간선의 값 return
	if (root->children.size() == 0) return root->weight;
	//자식이 하나일 경우 자신의 weight을 더해 return
	if (root->children.size() == 1) 
		return root->weight + traverse(root->children[0]);
	
	//여기서부터는 자식이 둘 이상
	vector<int> weights = vector<int>(root->children.size());

	//자식들 모두 다 돌때까지
	for (int i = 0; i < root->children.size(); i++) 
		weights[i] = traverse(root->children[i]);
	
	//오름차순으로 정렬
	sort(weights.begin(), weights.end());

	//가장 큰 값을 가진 두 값을 더해서 value와 비교하여 value업데이트
	value = max(weights[root->children.size()-1]
		+ weights[root->children.size()-2], value);
	
	//현재의 weight와 다 더한값의 제일큰 weights값을 더하여 return
	return root->weight+weights[root->children.size()-1];
}

int main() {
	
	scanf("%d", &n);
	nodes[1] = Node();
	nodes[1].weight = 0;
	n--;
	for (int i = 0; i < n; i++) {
		int from, to, weight;
		scanf("%d %d %d", &from, &to, &weight);
		nodes[to] = Node();
		nodes[to].weight = weight;
		nodes[from].children.push_back(&nodes[to]);
	}
	int ret = max(value, traverse(&nodes[1]));
	printf("%d\n", ret);
}

이상으로 트리에 관한 문제를 풀어보았습니다.