이분 매칭(bipartite matching)
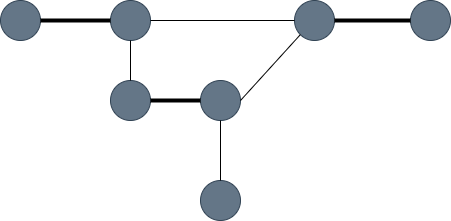
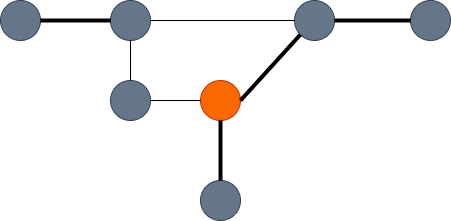
그래프에서 정점의 짝을 이루게 해볼까요? 정점은 다른 정점과 짝이 될 수 있는데, 단 여기서 한 정점은 최대 한 정점과 짝을 이룰 수 있는 조건으로 말이죠. 정점이 모두 선택될 필요는 없습니다. 아래의 그래프가 그 예를 보여줍니다. 왼쪽은 1:1 매칭이 된 간선을 선택한 것이고 오른쪽은 1:1 매칭이 되지 않은 그래프입니다. 왼쪽의 그래프는 간선을 3개 갖는데 각 정점은 1:1로 짝을 이루고 있네요. 하지만 오른쪽 그래프에서 주황색 정점은 위, 아래 정점 2개와 짝을 이루고 있으니 1:1 매칭이 되었다고 볼 수 없습니다.
 |
 |
정점을 보기좋게 두 그룹으로 나누면 어떨까요? 왼쪽에 정점이 오른쪽에 정점과 연결될 수 있도록 보면 더 보기 편할 거 같습니다.
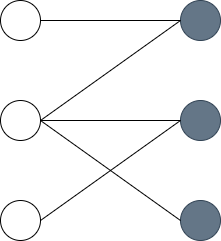
이처럼 그래프의 정점을 두 그룹으로 나눈 후 모든 간선이 서로 다른 그룹의 정점들을 연결할 수 있는 그래프를 이분 그래프라고 합니다. 여기서 가장 큰 매칭을 찾아내는 문제를 최대 매칭 문제(Maximum Matching)라고합니다. 간단하게 이분 매칭이라고 부릅니다.
이분 매칭을 네트워크 유량을 이용하여 풀게 됩니다. 그보다는 아주 간단하게 dfs를 이용해서 풀 수 있습니다. 이분 매칭을 구현한 코드가 아래에 있습니다. (이 코드는 구종만 님의 알고리즘 문제해결 전략의 코드입니다.)
#include<iostream>
#include<algorithm>
#include<vector>
#include<string.h>
using namespace std;
const int MAX_N = 201;
int adj[MAX_N][MAX_N];
vector<bool> visited;
vector<int> partner;
int N, M;
bool dfs(int here) {
if (visited[here]) return false;
visited[here] = true;
for (int there = 1; there <= M; there++) {
if (adj[here][there]) {
//there의 짝이 정해지지 않았거나
//there의 짝이 다른짝과 매칭된다면 true반환
if (partner[there] == -1 || dfs(partner[there])) {
partner[there] = here;
return true;
}
}
}
return false;
}
int bipartiteMatch() {
int ret = 0;
for (int i = 1; i <= N; i++) {
visited = vector<bool>(N + 1, false);
if (dfs(i)) ret++;
}
return ret;
}
왼쪽의 정점은 A, 오른쪽의 정점은 B라고 칭한다면 partner라는 배열은 B와 짝이된 A정점을 뜻합니다. 초기화는 아래와 같이 -1로 초기화시킵니다. partner[b]가 -1이면 아직 짝이 정해지지 않은 정점을 의미합니다.
partner = vector<int>(M + 1, -1);
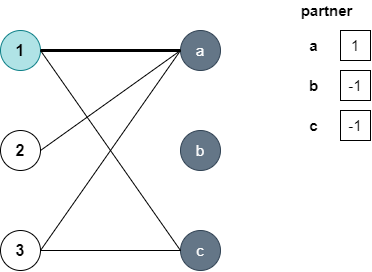
전체적으로 보면 왼쪽(here)에서 하나 씩 dfs를 탐색하는데요. dfs를 통해 짝을 찾을 수 있다면 매칭된 수를 하나 증가시킵니다. 코드와 글로는 이해가 어렵습니다. 그림이 있어야겠네요. 처음에 파란색 정점이 dfs를 수행합니다. 이때 조건문을 잘보세요. 설명을 편하게 하기 위해서 왼쪽 정점은 숫자, 오른쪽 정점은 알파벳으로 가정하도록 하겠습니다.
if (adj[here][there]) {
//there의 짝이 정해지지 않았거나
//there의 짝이 다른짝과 매칭된다면 true반환
if (partner[there] == -1 || dfs(partner[there])) {
partner[there] = here;
return true;
}
}
정점 1은 정점 a와 연결이 되고 있고(adj[1][a]), partner[a]의 짝은 아직 정해지지 않았으니, partner[a]=1이 되고 dfs는 true를 반환합니다. 그러니 짝을 하나 찾았네요.
이제 2번에서 dfs를 수행합니다. 연결된 간선의 정점이 a인데, a는 이미 짝이 있으나, a의 파트너인 1이 다른 짝과 매칭될 수 있는지(dfs(1))을 보는데요. 1은 다시 a로 가려고 하지만 이미 방문된 정점(visited[a]=true)이기 때문에 다른 연결된 c쪽으로 탐색합니다. c는 아직 짝이 정해지지 않았기 때문에 c의 파트너를 1로 정합니다. 그 결과 a의 파트너는 3이 될 수 있네요.
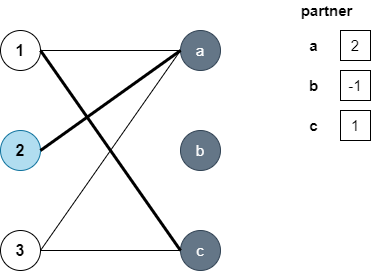
이제 다음 정점인 3에서 dfs를 시작합니다. 연결된 정점은 a와 c인데요. a는 이미 짝이 정해져있으나, partner[a]에서 dfs를 수행하면 다른 짝을 구할 수도 있으니 dfs(partner[a]) = dfs(1)를 수행합니다. dfs(1)은 dfs를 수행하지 않은 c로 탐색을 수행할텐데, 이때 c와 유일하게 연결된 정점 3은 이미 방문된 상태이므로 결국 다른 짝을 찾지 못했습니다.
이제 3의 다른 정점 c도 역시 같은 방법으로 경로를 찾는데 c는 이전에 방문되었던 상태라서 종료합니다. 결국 3에서 dfs를 수행한 결과 다른 짝을 찾지 못했네요.
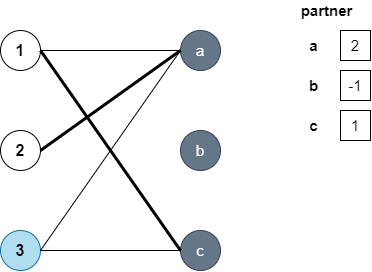
결국 이렇게 이분 그래프에서 최대 2쌍을 찾을 수 있습니다.
예제(BOJ 2188 축사배정)
2188번: 축사 배정
농부 존은 소 축사를 완성하였다. 축사 환경을 쾌적하게 유지하기 위해서, 존은 축사를 M개의 칸으로 구분하고, 한 칸에는 최대 한 마리의 소만 들어가게 계획했다. 첫 주에는 소를 임의 배정해
www.acmicpc.net
이 문제는 위의 코드를 그대로 구현하여 풀 수 있습니다. N마리의 소와 M개의 축사가 있는데, 각 소들은 들어가길 희망하는 축사가 있어 그 외의 축사는 들여보낼 수 없습니다. 소가 희망하는 축사는 여러개가 될 수 있는데요. 이때 소를 최대한으로 들여보낼 수 있는 수를 구하는 것입니다. (1<= N,M <= 200)
첫줄에는 N,M을 입력으로 받고 그 다음부터 차례대로 N 줄까지 1번 소가 원하는 축사의 수, 축사의 번호를 차례대로 입력받습니다. 그때 입출력의 예는 아래와 같습니다.
| 입력 | 출력 |
| 5 5 2 2 5 3 2 3 4 2 1 5 3 1 2 5 1 2 |
4 |
이 문제를 해결할 수 있는 전체 코드는 아래와 같습니다.
#include<iostream>
#include<algorithm>
#include<vector>
#include<string.h>
using namespace std;
/*이분매칭
소와 방을 1:1로 짝을 지을 수 있는 최대수를 반환
*/
const int MAX_N = 201;
int adj[MAX_N][MAX_N];
vector<bool> visited;
vector<int> partner;
int N, M;
bool dfs(int here) {
if (visited[here]) return false;
visited[here] = true;
for (int there = 1; there <= M; there++) {
if (adj[here][there]) {
//there의 짝이 정해지지 않았거나
//there의 짝이 다른짝과 매칭된다면 true반환
if (partner[there] == -1 || dfs(partner[there])) {
partner[there] = here;
return true;
}
}
}
return false;
}
int bipartiteMatch() {
int ret = 0;
for (int i = 1; i <= N; i++) {
visited = vector<bool>(N + 1, false);
if (dfs(i)) ret++;
}
return ret;
}
int main() {
cin >> N >> M;
partner = vector<int>(M + 1, -1);
for (int from = 1; from <= N; from++) {
int n;
cin >> n;
for (int i = 0; i < n; i++) {
int to;
cin >> to;
adj[from][to] = 1;
}
}
cout << bipartiteMatch() << endl;
return 0;
}
이상으로 그래프 이분 매칭에 대한 개념과 예제 코드였습니다.
'알고리즘 > DFS' 카테고리의 다른 글
| [DFS] 위상정렬(Topological Sort)의 세부 설명 및 코드(C++) (0) | 2021.03.11 |
|---|---|
| [알고리즘] 백준 온라인 저지 BOJ 2667 단지번호붙이기 풀이 및 코드 (0) | 2019.03.23 |
| [알고리즘] 백준 온라인 저지 BOJ 1260 DFS와 BFS (0) | 2018.09.19 |
| [알고리즘 DFS] 백준 온라인 저지 (BOJ) 1012 유기농 배추 (0) | 2018.09.18 |
| [알고리즘 : 그래프 이론] 그림으로 쉽게 보는 DFS 기본, 개념, 설명, 코드 (0) | 2018.09.12 |



