'이분탐색'에 해당되는 글 1건

BOJ 2805 나무 자르기

www.acmicpc.net/problem/2805

설명

1박 2일의 상근이가 나무가 필요한데, 벌목하고 잘린 나무를 사용한다는 내용입니다. 이때 벌목할때 쓰는 목재절단기는 한번에 H만큼 높이까지 모든 나무를 한번에 자를 수 있다고 합니다. 환경을 생각하는 상근이는 나무가 최대한 잘려나가지 않고 필요한 나무를 얻어내는것이 목표입니다.

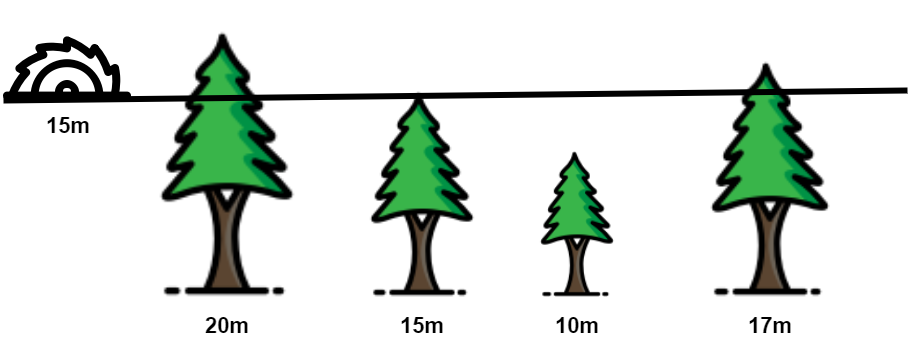
만약 나무 4개가 20m, 15m, 10m, 17m가 있고 상근이가 필요한 나무는 7m일때 목재절단기의 높이가 15m가 되면 첫번째 나무에서 5m, 네번째 나무에서 2m를 얻어낼 수있으므로 잘리는 높이를 15m로 정해주어야하죠. 필요한 나무를 다 채우면서 나무를 최대한 높게 자르려면 절단기의 높이를 어떻게 정해야할까요?

풀이

나무의 수 N과 구하고자 하는 상근이의 나무 M이 주어지고 범위가 1<= N <= 1,000,000, 1<= M <= 2,000,000,000입니다. 보통 이런식으로 말도 안되는 큰 값을 범위로 주면 log가 섞여있는 알고리즘으로 풀어야합니다. 떠올려볼 수 있는 알고리즘이 빠른 정렬 알고리즘, 이진탐색 등이 있겠네요.

우선 중간 정도의 높이 정해보고 만약 상근이가 가져갈 수 있는 양이면 점차적으로 높이를 높이는 방식으로 접근하면 됩니다. 

어떤 높이 height가 주어졌을때 이 height로 잘린 트리의 남은 부분을 전부 합쳐 M 이상이면 이 height는 H의 조건을 만족하게 됩니다. 이 함수가 아래의 isPossible이지요.

bool isPossible(unsigned int height) {
	unsigned int taken = 0;
	for (int i = 0; i < N; i++) {
		if (trees[i] >= height)
			taken += (trees[i] - height);
		if (taken >= M) return true;
	}
	return false;
}

그래서 만약 그 높이가 가능하다면 높이를 올립니다. 그리고 다시 가능한지 확인하죠. 아래의 코드는 이진탐색의 코드입니다.

isPossible에서 true가 반환되었다면 일단 답이 될 후보이며 ret에 그 값을 저장해놓습니다. 그리고 left의 값을 mid + 1로 증가시켜 자를 높이를 높게만들죠. isPossible이 false가 반환되었다는 것은 이 값은 답 후보가 아니라는 겁니다. 그래서 자를 높이를 아래로 조정합니다.

right는 입력에서 들어올 수 있는 가장 큰 값으로 지정을 했는데, 정석대로 풀려면 나무들을 순회하면서 가장 큰 나무의 높이가 right가 되어야겠죠? 하지만 이진탐색은 빠르니까 가장 큰 값을 지정해도 문제는 없습니다.

int solve() {
	unsigned int left = 0, right = 1000000000;
	unsigned int mid,ret;
	while (left <= right) {
		mid = (left + right) / 2;
		if (isPossible(mid)) {
			ret = mid;
			left = mid + 1;
		}
		else {
			right = mid - 1;
		}
	}
	return ret;
}

그리고 이진 탐색에서 나무들은 모두 정렬된 상태여야합니다. 그래서 문제를 풀기 전에 sort로 정렬합니다. 아래는 전체 코드입니다.

#include <iostream>

using namespace std;
int N;
long long M;
long long trees[1000001];
bool isPossible(unsigned int height) {
	unsigned int taken = 0;
	for (int i = 0; i < N; i++) {
		if (trees[i] >= height)
			taken += (trees[i] - height);
		if (taken >= M) return true;
	}
	return false;
}
int solve() {
	unsigned int left = 0, right = 1000000000;
	unsigned int mid,ret;
	while (left <= right) {
		mid = (left + right) / 2;
		if (isPossible(mid)) {
			ret = mid;
			left = mid + 1;
		}
		else {
			right = mid - 1;
		}
	}
	return ret;
}
int main() {
	cin >> N >> M;
	for (int i = 0; i < N; i++)
		cin >> trees[i];

	cout << solve() << endl;

}

위 풀이의 시간은 O(N log(M)) 입니다. isPossible은 모든 나무를 돌아가며 연산하기 때문에 N, 그리고 이진 탐색의 뼈대인 solve함수가 log M이 되죠.