위상 정렬(Topological Sort)
위상 정렬은 무엇일까요? 여러 작업들이 있을때 특정 작업을 수행하기 전 진행되어야 할 작업들이 있을텐데요. 이 작업들을 순서에 맞게 정렬해주는 것이 바로 위상정렬이라고 합니다. 이때 각 작업들은 직전 작업에 의존하게 되죠. 예를 들어 C라는 작업을 끝내기 위해서는 A작업과 B작업이 끝나야지만 C작업을 시작할 수 있는데, C는 A와 B가 끝날때까지 일을 실행하지 못하므로 A와 B에게 의존하고 있다고 봐야겠죠.
위상정렬은 우리 삶에도 영향이 있습니다. 예를 들어 요리할때나 청소할때, 여러분이 좋아하는 게임을 할때도 일의 순서등 말이죠.
위상정렬은 깊이 우선 탐색(Depth First Search, DFS)로 풀 수 있는 대표적인 정렬 방법입니다. 여기서 그래프는 의존성 그래프(Dependency Graph)의 모양을 띄고 있어야하는데, 그 말은 각 정점(작업)의 의존 관계를 간선으로 나타낸 방향 그래프라는 의미입니다. 만일 작업 v는 u가 끝나야만 수행할 수 있다면(v가 u에 의존한다면), 그래프는 u->v로 향하는 간선을 포함하게 됩니다. 의존성 그래프에서는 사이클이 존재할 수 없습니다.
자, 여기 작업을 나타내는 의존성 그래프가 있습니다.
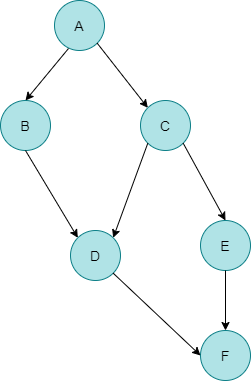
위상정렬 순서 단계별 알아보기
작업 순서)
B와 C는 A가 작업을 끝나야만 실행 가능
D는 B와 C가 작업을 끝나야만 실행 가능
E는 C가 끝나야만 실행 가능
F는 D와 E가 작업을 끝나야만 실행 가능
만약 여기서 F가 A로 향하는 간선이 있다면 어떻게 될까요? 그렇다는 의미는 A는 F 다음으로 수행가능 하다는 것인데, A는 이미 수행했기 때문에 모순입니다. 그렇기 때문에 의존성 그래프에는 사이클이 발생하지 않습니다. 이 그래프를 보기좋게 옆으로 돌려보도록 하겠습니다. 그러면 아래의 모양이 나오겠네요.
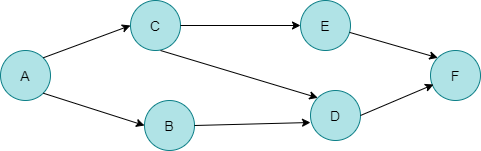
DFS를 이용해서 이 그래프의 위상정렬을 하면 결과는 이렇습니다. A C E B D F
여기서 힌트는 DFS를 종료한 역순이라는 것이 위상정렬된 결과라는 점입니다. 글로는 이해가 어려울 수 있으니, 이제 DFS를 통해서 어떻게 이 그래프가 위상 정렬이 되는지 그 과정을 보도록 합시다. 그전에 DFS를 방문할 노드의 규칙을 다음과 같이 정합시다. 연결된 정점 중 알파벳 순서가 가장 낮은 정점부터 탐색하는 것으로요.
1. 들어오는 간선이 없는 A부터 DFS 탐색을 실시하면 아래의 그림과 같이 F에서 끝이 납니다. F는 이때 더 이상 나가는 간선이 없으니까 F는 종료가 됩니다. - 종료 순서 F
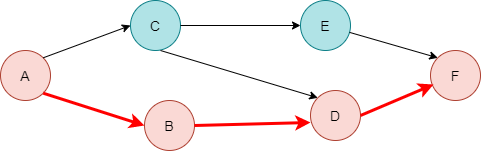
2. F가 반환되면 D가 다음 종료됩니다. 여기서 D에서 더 이상 방문할 정점이 없으니까요. - 종료 순서 F D
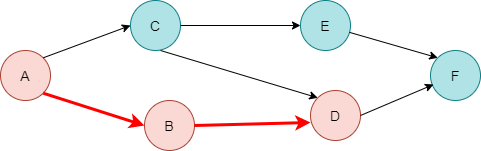
3. B역시 마찬가지로 종료됩니다. - 종료 순서 F D B
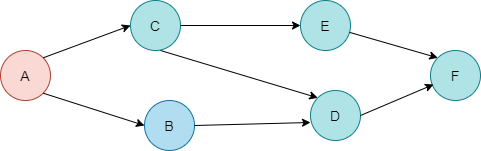
4. 이후 A는 종료되지 않습니다. 왜냐면 C와 연결된 정점이 있으니까요. 그래서 결국 E까지 DFS가 탐색을 하여 도달하게 됩니다. E는 더이상 방문할 노드가 없습니다. 그러니 종료하게 됩니다. - 종료 순서 F D B E
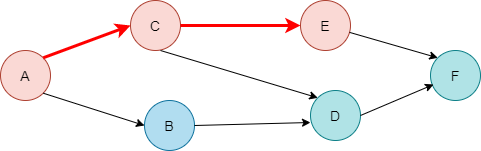
5. C는 D와 연결된 간선이 있는데 이전에 D는 방문 됐었죠? 그러니 C도 더 이상 방문할 정점이 없으니 종료됩니다. - 종료 순서 F D B E C
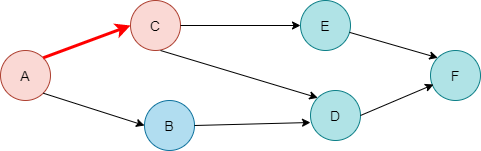
6. 이제 A는 더 이상 방문할 노드가 없으니 종료됩니다. 종료 순서 F D B E C A

DFS가 종료된 순서는 F D B E C A 인데, 이 순서를 역으로 취하면 A C E B D F 입니다. 어때요? 우리가 원하는 결과를 얻을 수 있죠?
그리고 아래의 코드는 위상정렬을 구현한 코드입니다.
#include <cstdio>
#include <algorithm>
#include <vector>
using namespace std;
int N,M;
vector<vector<int> > adj;
vector<bool> visited;
vector<int> order;
void dfs(int here) {
visited[here] = true;
for (int there = 0; there < adj.size(); there++) {
if (adj[here][there] && !visited[there])
dfs(there);
}
//위의 정점이 다 종료된 후에 이 곳의 정점(here)이 추가가 되어야함
order.push_back(here);
}
void topologicalSort() {
int n = adj.size();
visited = vector<bool>(N, false);
order.clear();
//들어오는 간선이 없을 경우가 있을 수 있으므로 모두 DFS 탐색
for (int i = 0;i<N;i++)
if (!visited[i]) dfs(i);
//종료된 순서를 거꾸로 만든다.
reverse(order.begin(), order.end());
}
void printOrder() {
for (int i = 0; i < order.size(); i++)
printf("%c ", order[i] + 'A');
printf("\n");
}
int main() {
printf("정점의 갯수 : ");
scanf("%d", &N);
printf("간선의 갯수 : ");
scanf("%d", &M);
visited = vector<bool>(N, false);
adj = vector<vector<int>>(N, vector<int>(N, 0));
for (int i = 0; i < M; i++) {
char from, to;
printf("정점1 -> 정점2 : ");
scanf(" %c %c", &from, &to);
adj[from-'A'][to-'A'] = 1;
}
topologicalSort();
printOrder();
}
topologicalSort안에 dfs를 전부 호출하는 이유는 아래의 그림과 같은 정점이 있을 수 있기 때문입니다. 여기서 G는 A와 같이 들어오는 간선(inboud-edge)이 없으므로 A부터 수행한 DFS에서는 G정점이 방문되지 않습니다. 그렇기 때문에 모든 정점을 방문하는 것입니다.
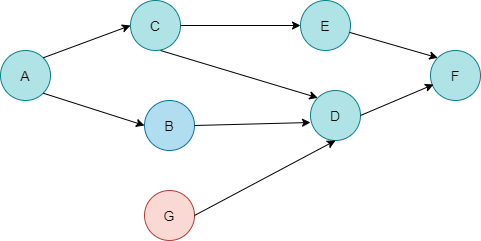
위의 코드를 실행한 결과를 보면 위상정렬이 잘 된 것임을 확인할 수 있습니다.
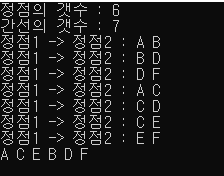
그리고 제가 제시했던 바로 위의 그래프의 위상정렬 결과는 아래와 같습니다.
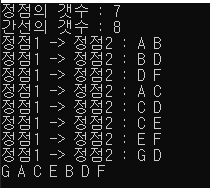
이상으로 위상정렬에 대해서 알아보았습니다. DFS의 응용이면서 결코 어렵지 않은 주제니까 원리와 코드는 알아두시면 좋겠습니다. 위의 코드는 구종만 저자님의 알고리즘 문제 해결 전략을 변형해서 만든 코드입니다.
'알고리즘 > DFS' 카테고리의 다른 글
| [그래프] 이분 매칭(bipartite matching)의 설명과 코드, 예제 (0) | 2021.03.06 |
|---|---|
| [알고리즘] 백준 온라인 저지 BOJ 2667 단지번호붙이기 풀이 및 코드 (0) | 2019.03.23 |
| [알고리즘] 백준 온라인 저지 BOJ 1260 DFS와 BFS (0) | 2018.09.19 |
| [알고리즘 DFS] 백준 온라인 저지 (BOJ) 1012 유기농 배추 (0) | 2018.09.18 |
| [알고리즘 : 그래프 이론] 그림으로 쉽게 보는 DFS 기본, 개념, 설명, 코드 (0) | 2018.09.12 |



