하한(Lower bound), 상한(Upper bound)
하한, 상한은 배열이 이미 정렬된 상태에서 적용되어야합니다. 상한, 하한은 모두 이진 탐색(Binary Search)로 구현이 되어있기 때문이죠. 여기서 이진 탐색은 아래의 코드인 것을 알고 계시겠죠? 이진 탐색의 기본 코드는 아래와 같습니다. 이진 탐색의 탐색 속도는 O(lg 2)의 속도를 자랑하지요.
int BinarySearch(int s, int e, int number)
{
int left=s,right=e,mid;
while (left <= right)
{
mid = (left + right) / 2;
if (arr[mid] == number) return mid;
if (arr[mid] > n) right = mid -1;
else left = mid + 1;
}
return -1;
}
하한이란? (Lower Bound)
특정 값 K보다 같거나 큰 값이 처음 나오는 위치가 됩니다. 즉, K값 이상인 값이 맨 처음 나오는 위치여야합니다. 아래는 그 예를 나타내는 표입니다. 이때 맨 앞 요소의 index는 0으로 시작합니다.
| 배열 1 2 2 4 4 5 6 6 6 9 9 |
lower_bound |
| lower bound( 4 ) | 3 |
| lower bound( 5 ) | 5 |
| lower bound( 9 ) | 9 |
하한을 Binary Search방식으로 구현한 코드는 아래와 같은데요. number값을 이상인 값이 mid 위치에서 발견되었다면 왼쪽으로 더 가다보면 아예 작은 수를 만나게 되고 left와 right의 역전 현상이 발생되어 멈춥니다. 멈추기 전에 우리는 가장 마지막에 arr[mid] >= number인 상황을 lower_bnd에 저장한 상황이죠.
int Binary_Search_Lower_Bound(int s, int e, int number)
{
int left=s,right=e,mid;
int lower_bnd = -1;
while (left <= right)
{
mid = (left + right) / 2;
if (arr[mid] >= number)
{
lower_bnd = mid;
right = mid - 1;
}
else left = mid + 1;
}
return lower_bnd;
}범위를 좁혀가는 상황을 그림으로 표현했습니다.
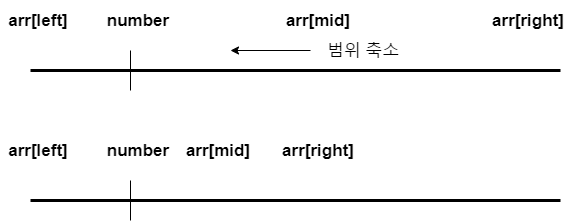
- C++의 lower_bound 사용
C++에서는 라이브러리 함수 형태로 lower bound를 지원합니다. 아래와 같은 형식을 사용하게 되는데요. 사용법은 이렇습니다.
lower_bound( 정렬한 배열 포인터, 정렬한 배열 포인터의 끝 주소, 값) - 정렬한 배열 포인터 |
여기서 정렬한 배열의 포인터는 알겠는데, 정렬한 배열 포인터의 끝 주소값은 어떻게 구할까요? 그냥 마지막 원소의 주소를 넣어주거나 배열의 주소 + 배열의 사이즈로 넣어주면 됩니다.
lower_bound의 반환 값은 하한값의 주소를 돌려주기 때문에 만약 index를 얻으려면 정렬한 배열 포인터를 빼주면 됩니다. 이 함수의 사용법은 밑의 예제 코드에서 upper_bound의 함수와 같이 사용해보도록 하겠습니다.
상한이란? (Upper Bound)
특정 값 K보다 큰 값이 처음으로 나오는 위치가 됩니다. 즉, K값 초과인 값이 맨 처음으로 나오는 위치입니다. 몇 가지 예를 들어볼까요?
| 배열 1 2 2 4 4 5 6 6 6 9 9 |
upper_bound |
| upper bound( 4 ) | 5 |
| upper bound( 5 ) | 6 |
| upper bound( 9 ) | -1 |
이 역시 Binary Search로 구현되는데요. 구현한 모습은 아래와 같습니다. 중간의 비교문이 반대로 됐음을 알 수 있죠? 이것은 arr[mid]의 값이 number의 이하일때 number와 최대한 같은 값의 index를 찾기 위함입니다.
int Binary_Search_Upper_Bound(int s, int e, int number)
{
int left=s,right=e,mid;
int upper_bnd=-1;
while (left <= right)
{
mid = (left + right) / 2;
if (arr[mid] <= number)
{
upper_bnd = mid;
left = mid + 1;
}
else right = mid - 1;
}
return upper_bnd+1 >= N ? -1: upper_bnd+1;
}
만약 이렇게 돼서 while루프가 멈추었다면 arr[upper_bnd]값은 number값 초과 직전의 값일 것입니다. 그렇다면 arr[upper_bnd+1]의 값은 number보다 큰 값일 테지요. 그래서 마지막 return에서 +1을 해주는데, 이것이 배열의 사이즈를 넘어갈 수 있으니까 사이즈 체크하여 return합니다.
C++에서 당연히 lower_bound함수가 존재하듯 upper_bound의 함수 역시 존재하며 사용법은 동일합니다. 단, 아래와 같이 사용할때 상한 값을 못찾아줄때도 있는데, 이때는 배열의 인덱스를 넘어가는 값을 갖게됩니다.
upper_bound(정렬한 배열 포인터, 정렬한 배열 포인터의 끝 주소, 값) - 정렬한 배열 포인터 |
이제까지 설명한 내용을 예제 코드를 통해서 확인해보세요. 직접 구현한 BinarySearch 형식의 upper_bound, lower_bound도 같이 구현되어있습니다.
#include <iostream>
#include <algorithm>
using namespace std;
int arr[100];
int N = 11;
int BinarySearchLowerBound(int s, int e, int number)
{
int left=s,right=e,mid;
int lower_bnd = -1;
while (left <= right)
{
mid = (left + right) / 2;
if (arr[mid] >= number)
{
lower_bnd = mid;
right = mid - 1;
}
else left = mid + 1;
}
return lower_bnd;
}
int BinarySearchUpperBound(int s, int e, int number)
{
int left=s,right=e,mid;
int upper_bnd=-1;
while (left <= right)
{
mid = (left + right) / 2;
if (arr[mid] <= number)
{
upper_bnd = mid;
left = mid + 1;
}
else right = mid - 1;
}
return upper_bnd+1 >= N ? -1: upper_bnd+1;
}
int main(void) {
arr[0] = 4; arr[1] = 2; arr[2] = 4; arr[3] = 1; arr[4] = 9;
arr[5] = 2; arr[6] = 6; arr[7] = 6; arr[8] = 6; arr[9] = 9, arr[10] = 5;
//정렬
sort(arr, arr + N);
printf("정렬된 배열\n");
for (int i = 0; i < N; i++) printf("%d ",arr[i]);
printf("\n");
printf("Lower Bound\n");
printf("%d lower bound:%d\n", 4, BinarySearchLowerBound(0, N - 1, 4));
printf("%d lower bound:%d\n", 5, BinarySearchLowerBound(0, N - 1, 5));
printf("%d lower bound:%d\n", 2, BinarySearchLowerBound(0, N - 1, 2));
printf("%d lower bound:%d\n", 1, BinarySearchLowerBound(0, N - 1, 1));
printf("%d lower bound:%d\n", 9, BinarySearchLowerBound(0, N - 1, 9));
printf("%d lower bound:%d\n", 4, lower_bound(arr, arr + N, 4) - arr);
printf("%d lower bound:%d\n", 5, lower_bound(arr, arr + N, 5) - arr);
printf("%d lower bound:%d\n", 2, lower_bound(arr, arr + N, 2) - arr);
printf("%d lower bound:%d\n", 1, lower_bound(arr, arr + N, 1) - arr);
printf("%d lower bound:%d\n", 9, lower_bound(arr, arr + N, 9) - arr);
printf("Upper Bound\n");
printf("%d upper bound:%d\n", 4, BinarySearchUpperBound(0, N - 1, 4));
printf("%d upper bound:%d\n", 5, BinarySearchUpperBound(0, N - 1, 5));
printf("%d upper bound:%d\n", 2, BinarySearchUpperBound(0, N - 1, 2));
printf("%d upper bound:%d\n", 1, BinarySearchUpperBound(0, N - 1, 1));
printf("%d upper bound:%d\n", 9, BinarySearchUpperBound(0, N - 1, 9));
printf("%d upper bound:%d\n", 4, upper_bound(arr, arr + N, 4) - arr);
printf("%d upper bound:%d\n", 5, upper_bound(arr, arr + N, 5) - arr);
printf("%d upper bound:%d\n", 2, upper_bound(arr, arr + N, 2) - arr);
printf("%d upper bound:%d\n", 1, upper_bound(arr, arr + N, 1) - arr);
printf("%d upper bound:%d\n", 9, upper_bound(arr, arr + N, 9) - arr); //배열의 인덱스 초과된 값이 나옴
}
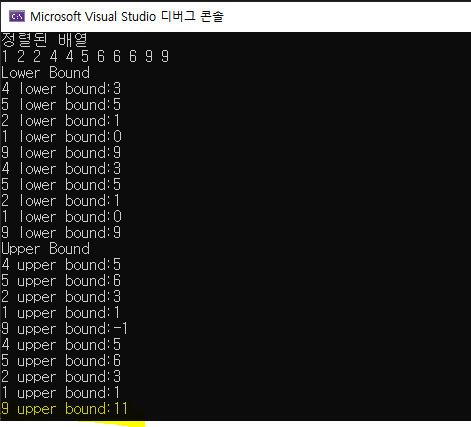
그리고 위 코드의 결과입니다. 마지막 upper_bound의 값이 다름을 확인해보세요.
'언어 > C++' 카테고리의 다른 글
| [C++] Map 개념과 사용방법, 예제 코드 + 백준 문제 풀이(BOJ 1764) (0) | 2022.03.28 |
|---|---|
| [C++] STL vector 개념과 정리 - 사용법 파헤치기 (0) | 2022.03.24 |
| [C++] new,delete 키워드와 오버라이딩(Overriding),다형성(Polymorphism)의 개념과 virtual키워드 사용방법, 객체의 this 포인터 개념 (0) | 2021.03.18 |
| [C++] 클래스와 상속(Inheritance)의 개념과 사용법, 캡슐화의 이해 (0) | 2021.03.16 |
| [C++]C++ 함수의 특징(오버로딩, 디폴트 인수, 참조자, 인라인 함수) (0) | 2019.05.06 |



