'백준온라인저지'에 해당되는 글 2건

14500번 주사위 굴리기

https://www.acmicpc.net/problem/14500

문제 해석

테트리스 게임을 조금 활용한 문제같습니다. 문제는 간단합니다.

어떤 판에 숫자들이 적혀있는데 여기서 테트리스모양으로 숫자를 골라 가장 최대가 나오는 값을 구하는 문제입니다.

테트리스 모양은 여러분들이 잘 아시죠? 여기서 물론 테트리스의 블록들은 4방향 회전이 가능합니다.

예제를 직접 풀어보도록 하지요. 아래의 문제의 첫번째 예제가 주어졌습니다.

여기서 가장 큰 수를 고르면 파랑색의 숫자들이 되겠습니다. 이 외에 더 큰 값을 테트리스 모양대로 고를수가 없는 것을 알 수 있습니다.

제약 조건

세로와 가로의 길이(N,M)은 4이상 500이하로 주어집니다. 입력으로 주어지는 수는 1000을 넘지 않는다고 합니다.

풀이

이 문제를 이전에 JAVA로 풀어놓은게 있으므로 이번 포스팅은 JAVA 코드로 구현했습니다.

가로와 세로의 길이는 최대 500이며, 숫자들은 모두 500x500으로 250,000개가 되겠네요. 또 이 중 최대 4개의 숫자만 더하면 되니 문제의 답은 총 4000을 초과하지 않습니다.

이와 같이 문제의 값의 범위가 적을때는 brute-force(전수조사)로 그 문제의 해답을 찾을 수 있습니다. 모든 가능한 수를 구하는 것입니다.

문제를 풀기에 앞서 손으로 테트리스 모양을 만듭시다. 총 7개의 모양을 가지고 있고, 4방향으로 회전을 하기 때문에 대략 28개의 테트리스 모양을 배열로 만들겁니다.

1은 블록이 있는 공간을 말하고 0은 블록이 없는 공간을 의미합니다. 이해가 더 잘가기 위해 아래 세가지 테트리스 블록을 그림으로 첨부했습니다.

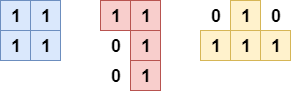
이제 이것을 배열로 만드는 것이죠. 이렇게 말이죠. 이 정도 약간의 노가다는 해도 괜찮아요. 시간이 그렇게 많지 않으니까요.

static int [][][]shapes={
		{{1,1,1,1}},{{1},{1},{1},{1}}, 
		{{0,1,0},{1,1,1}},{{1,1,1},{0,1,0}},{{0,1},{1,1},{0,1}},{{1,0},{1,1},{1,0}},
		{{1,1,1},{1,0,0}},{{0,0,1},{1,1,1}},{{1,1},{0,1},{0,1}},{{1,0},{1,0},{1,1}},
		{{1,1,1},{0,0,1}},{{1,0,0},{1,1,1}},{{0,1},{0,1},{1,1}},{{1,1},{1,0},{1,0}},
		{{1,1},{1,1}},
		{{1,0},{1,1},{0,1}},{{0,1,1},{1,1,0}},
		{{0,1},{1,1},{1,0}},{{1,1,0},{0,1,1}}
};

배열 첫번째 모양은 일자모양(l)이고, 두번째는 ㅗ모양입니다. 세번째 모양은 L자 모양이 되겠습니다. 이것을 사방으로 회전하다 보니까 2차원 배열이 한 줄에 최대 4개까지 나오며, 일자모양과 정사각형 모양 등 네 방향으로 회전할때 같은 모양이 나올 경우는 4개까지 나오지 않지요.

실제 문제를 푸는 코드는 아래에 있습니다. 

static int maxValue(int y,int x){
		int max=0;
		for(int next=0;next<19;next++){
			int r=shapes[next].length;
			int c=shapes[next][0].length;
			if(y+r>n||x+c>m) continue;
			int sum=0;
			for(int i=y;i<y+r;i++) for(int j=x;j<x+c;j++)
				sum+=map[i][j]*shapes[next][i-y][j-x];
			max=Math.max(max, sum);
		}
		return max;
	}

인자로 받은 y와 x는 비교할 위치를 말합니다. y는 세로축, x는 가로축의 좌표라고 보면 됩니다.

우리는 회전해서 나온 각각의 모양 19개(3차원 배열속의 2차원 배열 갯수)를 위에서 만들었지 않았나요? 그러니 for문을 19번 반복을 하는 겁니다.

이 for문 안에 r과 c는 만들었던 모양의 가로 길이, 세로 길이를 나타냅니다. 만약 {{ 0,1,0 }, { 1,1,1 }}의 (ㅗ)모양이라면 r의 값은 2, c의 값은 3이 되는 겁니다. 이런 길이가 입력 받은 보드의 범위를 넘어가게 되면 구할 필요가 없어지지요.

그런 조건을 if문으로 거릅니다.

int r=shapes[next].length;
int c=shapes[next][0].length;
if(y+r>n||x+c>m) continue;

범위 안에 있다면 이제 더해주면 됩니다. 우리가 블록이 있는 경우에는 1을 저장했었죠? 블록이 없는 경우는 0을 저장했었습니다. 그래서 판의 숫자에 이 이차원 배열을 단지 곱해주면 됩니다. 이 값을 모두 더하는 것이죠.

sum+=map[i][j]*shapes[next][i-y][j-x];

이제 모든 판의 좌표를 돌면서 가장 큰 값을 구하면 그게 답이 되는 겁니다. 전체 코드는 아래에 있습니다.

import java.util.Scanner;
public class Main {

	static int n,m;
	static int [][]map;
	static int [][][]shapes={
			{{1,1,1,1}},{{1},{1},{1},{1}}, 
			{{0,1,0},{1,1,1}},{{1,1,1},{0,1,0}},{{0,1},{1,1},{0,1}},{{1,0},{1,1},{1,0}},
			{{1,1,1},{1,0,0}},{{0,0,1},{1,1,1}},{{1,1},{0,1},{0,1}},{{1,0},{1,0},{1,1}},
			{{1,1,1},{0,0,1}},{{1,0,0},{1,1,1}},{{0,1},{0,1},{1,1}},{{1,1},{1,0},{1,0}},
			{{1,1},{1,1}},
			{{1,0},{1,1},{0,1}},{{0,1,1},{1,1,0}},
			{{0,1},{1,1},{1,0}},{{1,1,0},{0,1,1}}
	};
	public static void main(String[] ar){
		Scanner in=new Scanner(System.in);
		n=in.nextInt(); m=in.nextInt();
		map=new int[n][m];
		for(int i=0;i<n;i++) for(int j=0;j<m;j++)
			map[i][j]=in.nextInt();
		int max=0;
		for(int i=0;i<n;i++) for(int j=0;j<m;j++)
				max=Math.max(maxValue(i,j), max);
		System.out.println(max);
	}
	static int maxValue(int y,int x){
		int max=0;
		for(int next=0;next<19;next++){
			int r=shapes[next].length;
			int c=shapes[next][0].length;
			if(y+r>n||x+c>m) continue;
			int sum=0;
			for(int i=y;i<y+r;i++) for(int j=x;j<x+c;j++)
					sum+=map[i][j]*shapes[next][i-y][j-x];
			max=Math.max(max, sum);
		}
		return max;
	}
}

이상으로 테트로미노 문제를 풀어보았습니다.

LCS(Longest Common Subsequence)

백준 9251번입니다. 문제는 이렇습니다.

임의의 두 수열에서 공통적으로 갖고 있는 가장 긴 부분 수열의 길이를 구하는 것이 문제입니다.

예를 들어 다음과 같은 두 수열이 있다고 합시다.

첫번째 수열과 두번째 수열의 공통수열은 다음과 같습니다.

이 외에도 여러가지 공통 수열이 있지만 가장 긴 수열은 4의 길이를 갖고 있는 ACAK입니다. 두 수열에서 LCS는 여러가지가 있지만 그 길이는 같지요.

제약조건

두 수열을 항상 대문자 알파벳으로 주어지고 각 수열의 길이는 1이상 10000이하입니다.

풀이

이 문제는 생각보다 단순합니다. 두 수열의 문자를 비교해 일치하면 동시에 한칸을 옮겨서 그 다음부터 비교하면 되고, 만약 일치하지 않는다면 두 수열중 아무것이나 한칸 옮겨서 그 다음부터 비교하면 됩니다.

위 두 수열의 LCS길이는 AKEPPA 또는 OKEPPA입니다. 그렇기때문에 답은 6이 나오지요. 이 답이 나오는 과정을 살펴보도록 하겠습니다.

빨간색 글자는 현재 비교할 두 문자입니다. 우선 초기상태이므로 A와 O가 비교됩니다. 두 문자가 일치하지 않으므로 A의 다음 문자를 비교하거나 O의 다음 문자를 비교합니다. 저는 일부러 답을 찾기 위해서 최적의 방법을 사용할 것이니 여러분들은 두 수열 중 어떤 수열을 먼저 한칸 더 옮기든지 상관없다는 것만 아시면 됩니다.

첫번째 수열의 비교 문자를 한칸 옮기니까 두 수열의 문자가 일치하는 군요. 그렇다면 두 수열의 비교문자를 다음으로 옮겨줍니다.

L과 C는 일치하지 않으므로 두 수열중 비교할 문자를 한칸 뒤로 옮깁니다.

이런식으로 이제 계속 비교하다가 보면 언젠가는 다음과 같은 상황이 발생합니다.

이제 K와 K를 비교할 때가 된거죠. K는 두 수열이 두 수열의 비교문자를 모두 다음 위치로 이동합니다.

E 역시 두 문자가 같으므로 다시 또 한칸 동시에 비교문자를 옮깁니다. 옮기고 난 후 보니까 P와 M은 일치하지를 않지요. 그러니까 둘 중 아무 수열이나 비교할 문자를 한칸 옮겨줍니다. 저는 답을 찾기위해 일부터 아래 수열의 비교문자를 한칸 더 옮기겠습니다.

이제 P는 두 수열 모두 같으니 다음 칸으로 옮겨줍니다. 계속 이런식으로 답을 찾으면 결국 다음과 같은 LCS가 나오게 되는 것이죠.

이 LCS는 OKEPPA이고 길이가 6인 것을 알 수 있습니다. 따라서 답은 6이 되는 겁니다.

DP적용

이렇게 답은 찾았는데요. 길이가 10000인 두 수열을 이런식으로 계속 비교하다가는 시간안에 답을 찾기가 힘듭니다. 우리가 자세히 살펴본다면 DP를 적용할 수 있다는 사실을 알 수 있는데요. 만일 수열에서 순서가 A와 O를 비교했는데 아래 배열의 비교 문자를 옮긴다면 A와 C를 비교하게되어 O를 빠뜨리고 가지요. 분명 O는 일치하는 문자임에도요. 

[1][2][3][4][5][6][7][8][9][10]

A O L D M K E P P A

[1][2][3][4][5][6][7][8][9][10]

O C A C K E M P P A

그래서 결국 KEPPA까지만 일치하게 된 상황에서 각 인덱스는 [6][5]입니다. 

따라서 [6][5]에서 가장 긴 수열은 5라고 기억하지요. 그리고 다시 이전으로 돌아가서 비교해야합니다. 그때는 순서를 바꿔 O가 일치하는 상황이 되죠.

[1][2][3][4][5][6][7][8][9][10]

A O L D M K E P P A

[1][2][3][4][5][6][7][8][9][10]

O C A C K E M P P A

이렇게 [6][5]까지 비교한다면 이미 기억해두었으니 제차 끝까지 비교하지 않고 [6][5]까지의 값 5를 반환하기면 하면 됩니다. 그리고 O는 일치했으므로 1을 더하는것이죠. 그래서 답이 6이 됩니다. 이렇게 DP를 적용해서 시간을 줄일 수 있습니다.

구현

다음의 코드는 LCS의 길이를 구하는 코드입니다. 위의 설명을 잘 이해했다면 코드 역시 이해하기가 훨씬 쉬울거에요.

#include <stdio.h>
#include <string.h>

#define MAX(a,b) a>b ? a:b
#define _CRT_SECURE_NO_WARNINGS
char a[1001], b[1001];
int n, m;
int dp[1001][1001];
int solve(int pos1, int pos2) {
	if (pos1 == n || pos2 == m) return 0;
	if (a[pos1] == b[pos2])
		return 1 + solve(pos1 + 1, pos2 + 1);

	int ret = 0;
	if (dp[pos1][pos2] != -1) return dp[pos1][pos2];
	ret = MAX(solve(pos1 + 1, pos2), solve(pos1, pos2 + 1));
	return dp[pos1][pos2] = ret;
}
int main() {

	scanf("%s %s", a, b);
	n = strlen(a); m = strlen(b);
	memset(dp, -1, sizeof(int) * 1001 * 1001);
	int ret = solve(0, 0);
	printf("%d\n", ret);
}

pos1은 첫번째 수열의 비교할 문자 위치, pos2는 두번째 수열의 비교할 문자위치를 말합니다. 만약 pos1과 pos2이 하나라도 수열 끝까지 갔다면 종료되는 것이죠. 이것이 기저 사례입니다.

앞서 말한것과 같이 첫번째 수열의 pos1위치의 문자와 두번째 수열의 pos2위치 문자와 비교해서 같다면 LCS의 길이 1을 더해주고 비교할 문자의 위치 pos1,pos2를 한 칸 증가시켜줍니다.

만약 일치하지 않는다면 둘 중 하나의 수열 비교문자(pos1 또는 pos2)만 한칸 증가시키고 둘 중 가장 큰 값을 반환하면 되죠.

나중에 return할때 메모이제이션으로 값을 업데이트 시키는 것은 잊지 말고 말이죠.